Clearance and Elimination

Take home messages

• Clearance is the volume of plasma completely and irreversibly cleared of drug per minute
• The half life is the time taken for the plasma concentration to drop to half of any initial value
• Redistribution is not elimination

Podcast episode

Pharmacokinetics

It's always a magical feeling when you see the milk of amnesia disappear into the cannula; the patient's eyes fluttering closed just thirty seconds later.

Clearly the drug has made its way from arm - or foot or wherever you've finally managed to cannulate - to brain where it then exerted its mysterious pharmacodynamic effects.

But what else is going on?

Where else does it go? How much actually reaches the brain? What happens afterwards? How much is too much and when should I give more? - these are questions of pharmacokinetics, or what the body does with the drug once it's inside.

There are four aspects to pharmacokinetics that you should always mention in any viva question on the topic:

• Absorption
• Distribution
• Metabolism
• Elimination

In this post we're looking at the last bit - the elimination that so often gets examined in the Primary FRCA exam.

Buckle up.

What is elimination?

Let's start with a very simple definition.

Elimination is the irreversible removal of drug from the plasma, through one or both of the following mechanisms:

• Physical removal from the body (excretion)
• Metabolism into inactive breakdown products

Just note that redistribution to other bits of the body does not count as elimination, because although the molecule has left the plasma, it is very much coming back to haunt us later (it's not irreversible), as we'll explain in a bit.

Most polar or water-soluble drugs are excreted by the kidneys, and some larger molecules can be excreted into the bile.

The kidneys aren't very good at dealing with fat-soluble, non-polar drugs, so these need to be metabolised into a polar, soluble molecule first, usually by the liver, where they can undergo phase 1 and phase 2 reactions.

That's all we're going to say about metabolism in this post - we'll cover metabolism in all its glory another time.

What actually happens to the drug?

If we inject a single intravenous bolus dose of a drug, and then measure the plasma concentration over time, it generally looks something like this.

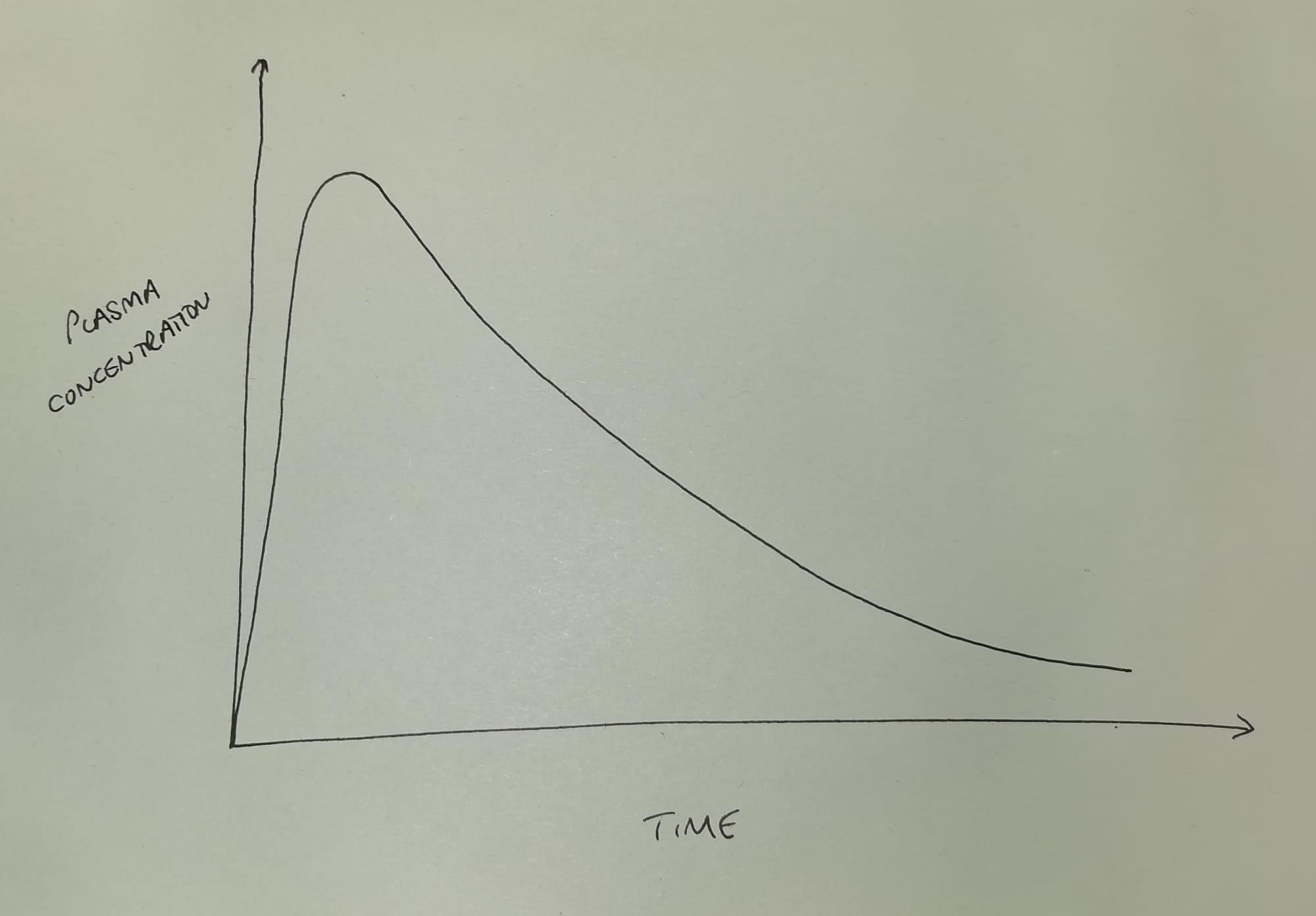
As you can see the plasma concentration initially shoots upwards as we inject the drug, and then rapidly starts to fall in an exponential manner as the drug is eliminated (and redistributed*) from the plasma.

• *for the time being, please ignore redistribution, and assume the body is a single compartment of fluid with the drug evenly distributed throughout - it'll allow us to focus on elimination, and generally make everyone's day so much easier.

Here, 'exponential' means that the gradient is becoming less steep as time goes on, and we have an equation for it.

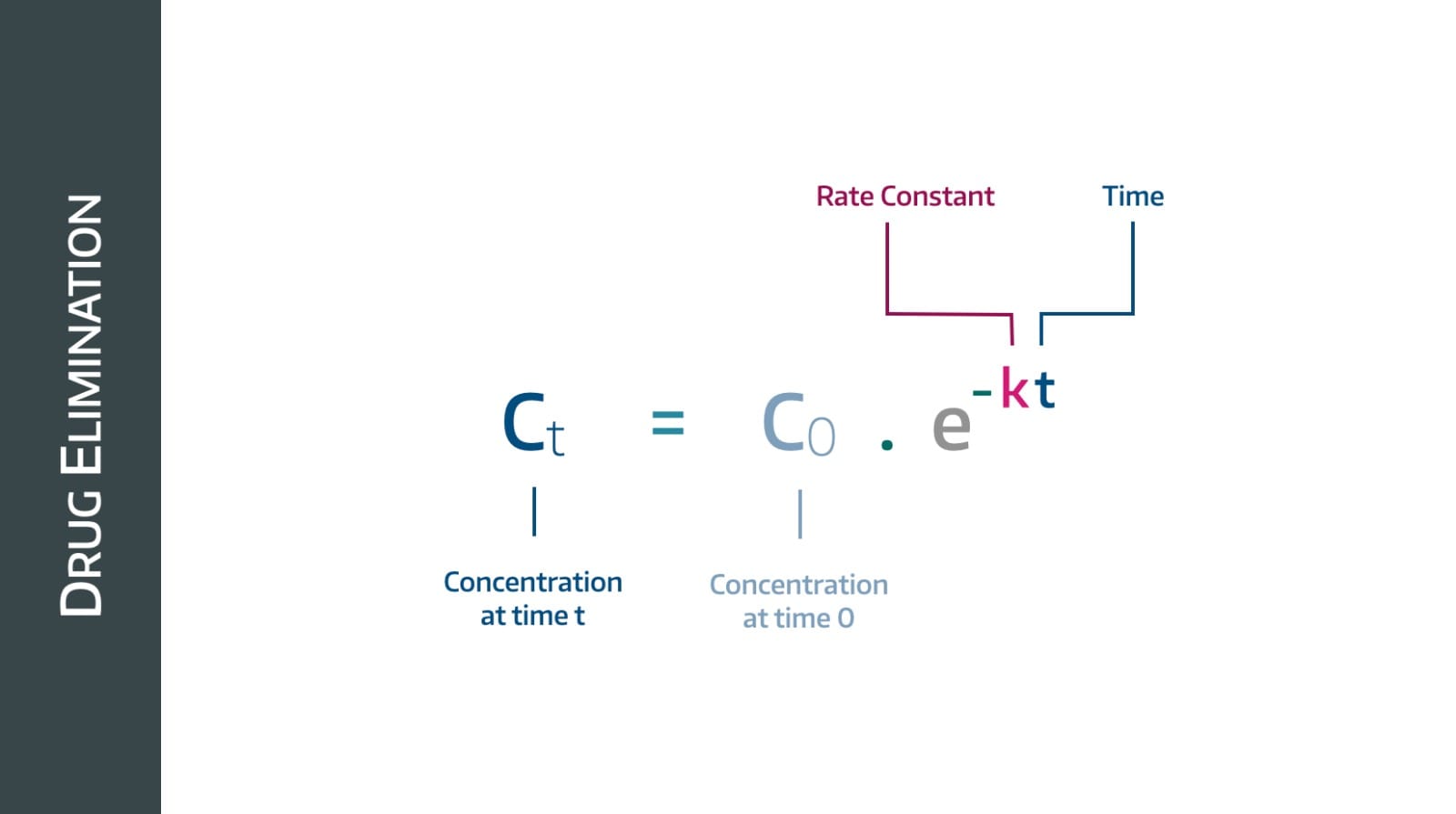
First order kinetics

This behaviour is called first order kinetics, and the vast majority of drugs follow this pattern.

The gradient here - by definition - is (change in plasma concentration)/time and in simple terms tells us the rate of drug removal in mg per minute.

Therefore we can see that the rate at which drug is removed over time is decreasing, which makes sense - to begin with there are loads of drug molecules for the kidneys to remove, and as their concentration drops, there are fewer available, so it takes longer.

What is special about the shape of this graph is this:

• The same proportion of drug is removed per unit time
• i.e. the plasma concentration drops by the same percentage over any given time period

Unfortunately this graph isn't a particularly helpful shape for doing calculations with, so we undertake some mathematical wizardry (we log it) and we get something like this:

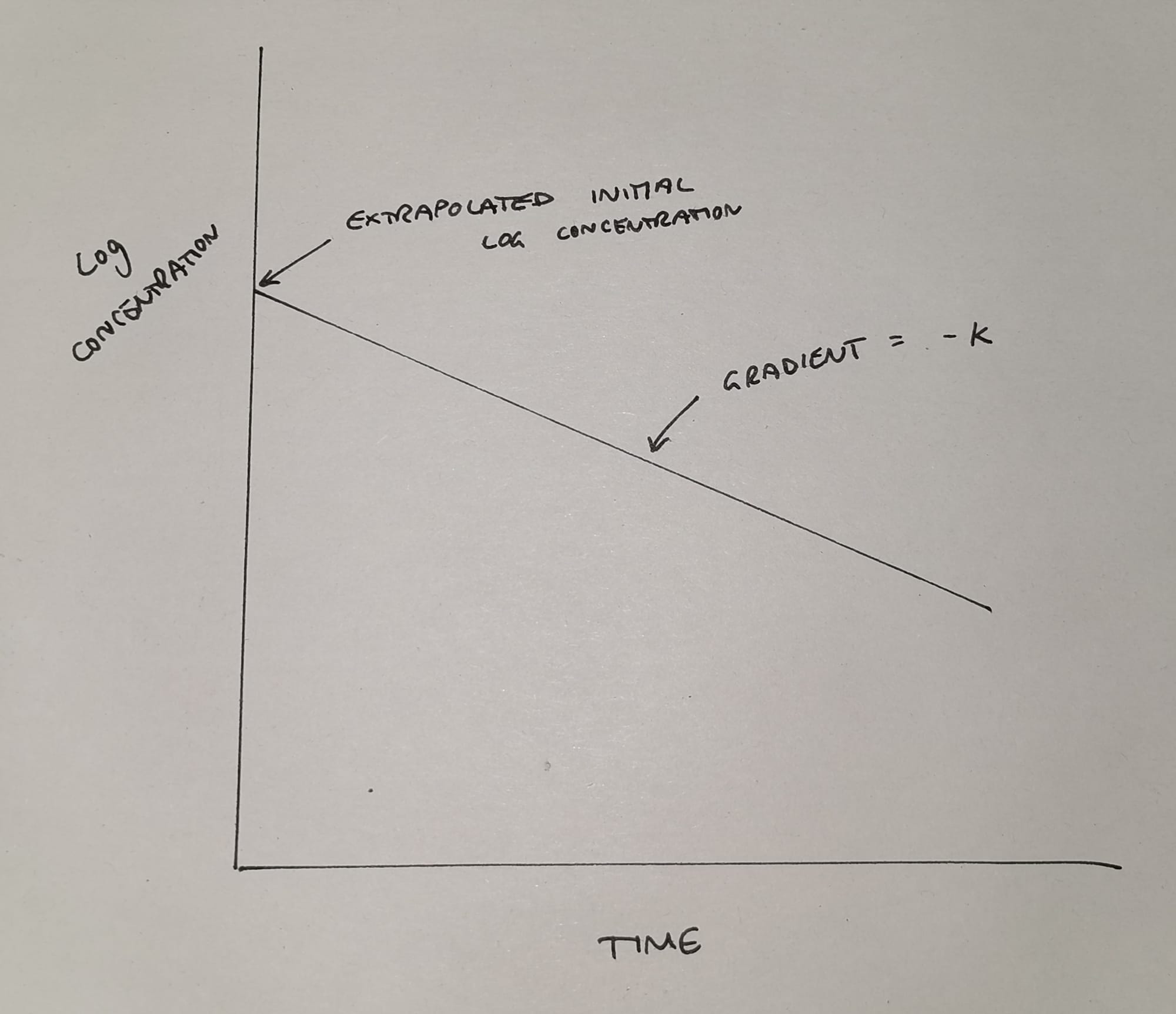
This much simpler graph now tells us two things:

• It allows us to work out the theoretical* initial plasma concentration
• It shows us the elimination rate constant k (the gradient of the slope)

*It's theoretical because it never actually happens - the drug starts being cleared from the blood while we're still injecting - but we like nice neat equations so we make it up using maths.

Now let me introduce you to k - the elimination rate constant.

You only need to know three things

There are three key concepts to understand when discussing elimination of a drug from the plasma:

• The elimination rate constant (k)
• The elimination time constant (τ pronounced 'tau')
• Half life (t_1/2)

A quick bit about zero order kinetics

We mentioned earlier that most drugs follow first order kinetics.

Compare the above graphs to this one:

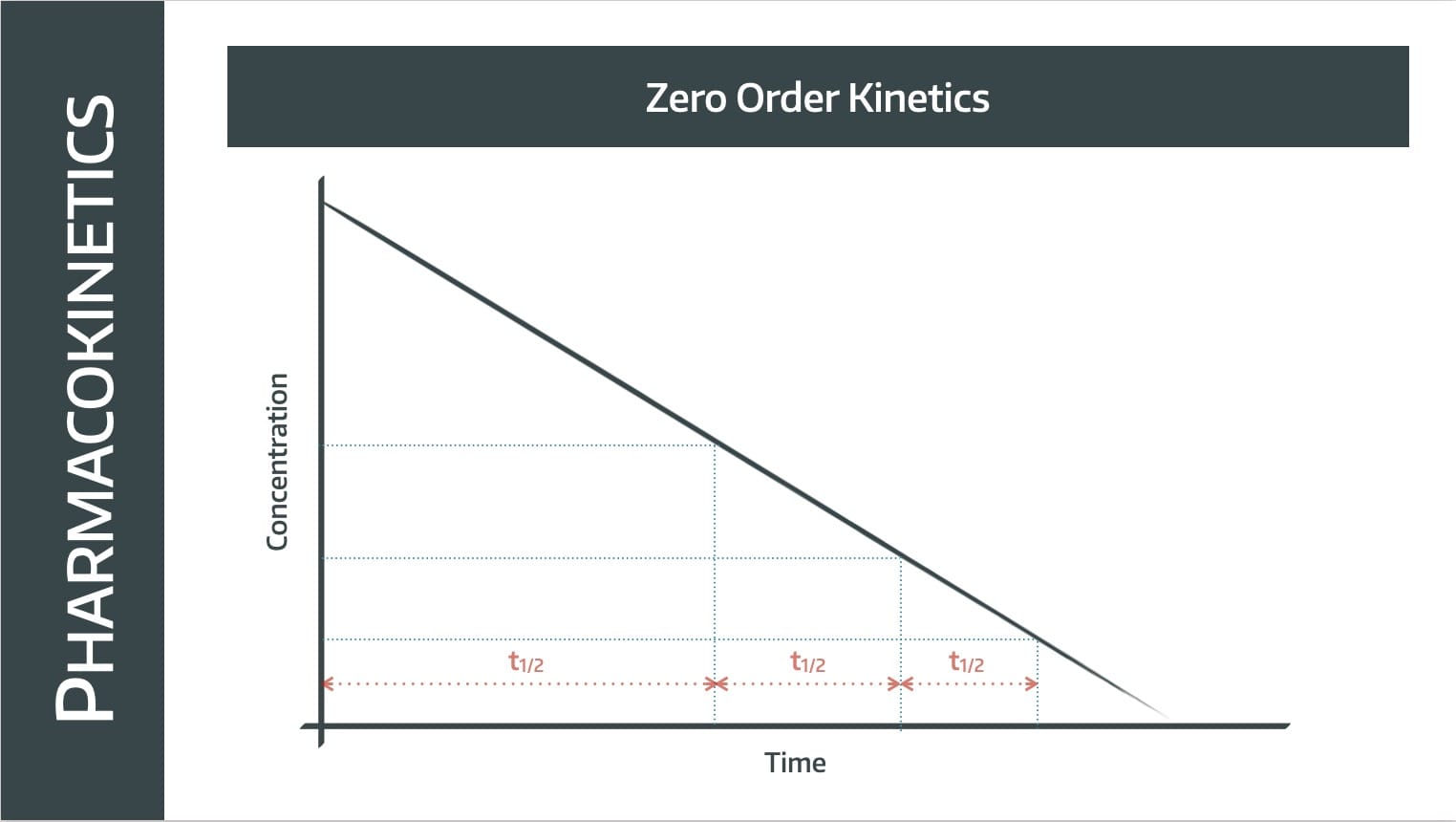
Note this is not a graph that we've log-ed, it's a concentration-over-time graph, which we'd usually expect to be a negative exponential.

In this situation however, the graph is a straight line with a constant gradient, meaning the rate of elimination is constant.

The same number of molecules are removed per unit time, so it takes twice as long to get from 100% to 50% as it does from 50% to 25%.

The half life gets shorter as plasma concentration decreases.

Zero order kinetics take place when the plasma concentration is no longer the limiting factor on rate of elimination, and this generally is seen in two circumstances:

• Massive overdose, with the enzymes completely overwhelmed (a.k.a. saturation kinetics)
• Specific weird drugs that do their own thing

The clinical importance of zero order kinetics is that only very small increases in administered dose can lead to dramatic and potentially harmful increases in plasma concentration.

That's quite enough about zero order kinetics I think.

If you've made it this far, then well done.

So far we've said:

• Elimination is the irreversible removal of drug from the plasma
• Most drugs follow first order kinetics
• This means their plasma concentration decreases exponentially over time
• Some drugs are weird and do their own thing

Now let's entertain the mad idea that we might actually want to measure elimination.

Rate of elimination

On the surface, rate of elimination would be a very sensible thing to measure - how much drug in mg or mmol is removed from the plasma per minute?

When we say 'removed' we include both physical removal of the molecule into urine, bile or faeces, or metabolism of the molecule to inactive metabolites.

As we mentioned earlier, we don't include redistribution into fat or other compartments, because those molecules can, and will, flood back into the plasma at some point later on.

Elimination means gone for good.

So when examining this process it initially makes logical sense to think about it in terms of 'amount of drug removed per minute'.

But we run into a problem

The problem here is that this number is going to change depending on the plasma concentration of the drug - as we mentioned earlier.

When there's a very large number of molecules hanging around, they can be eliminated very quickly - assuming your enzymes and transporters haven't reached maximum capacity and been overwhelmed - but as drug plasma concentration drops, so too does the rate at which its molecules are removed.

This means that rate of elimination is going to vary with plasma concentration.

And so that's why we use clearance instead.

Say hello to Clearance

At first glance, this seems like a strange metric to use to measure the efficiency of drug elimination, but the reason we like it is because it remains constant regardless of plasma concentration.

To do this, it takes into account the volume into which the drug is distributed, and it give us the following equation:

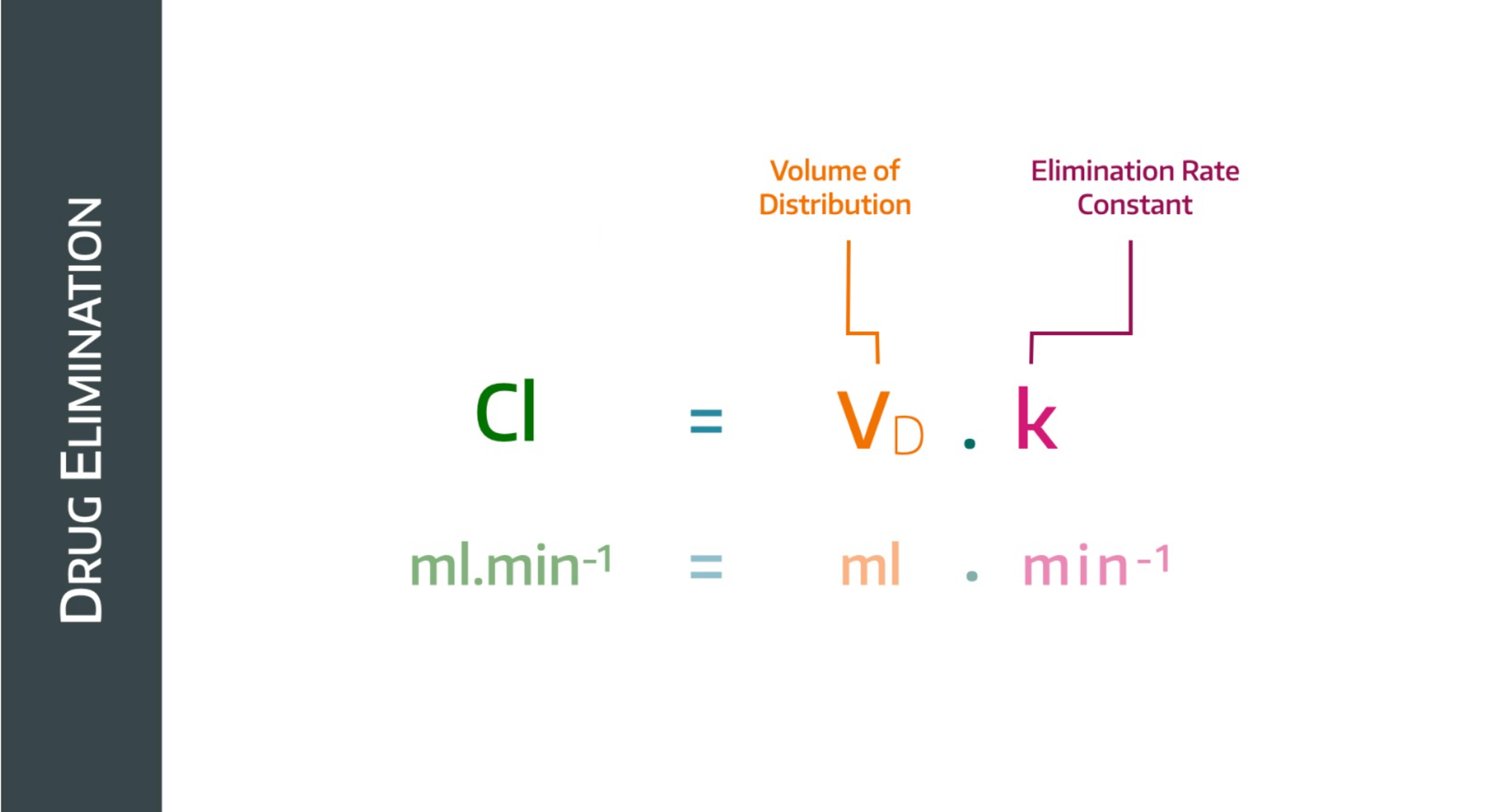
If the plasma concentration drops, then the rate constant will drop too, but the volume of distribution will increase (because a lower concentration implies a higher volume of distribution)

Clearance is therefore essentially the proportionality constant linking rate of elimination to plasma concentration.

There are types of clearance

This bit is very simple - the total clearance for the body is a sum of all the separate little bits of clearance carried out by different organs.

• Unsurprisingly, renal clearance tends to be the biggest
• Hepatic clearance is also important
• Other organs are usually forgotten about

This is important to know, because if a drug is predominantly renally cleared, then we need to adjust the dose in renal impairment, whereas if a lot of the work is done by the liver, we probably don't need to worry quite so much.

Alternative ways to calculate clearance:

Why do I care about rate of elimination or clearance?

Because if you want to give an infusion at a steady plasma concentration, you need to know how quickly to infuse the drug.

• Maintenance infusion rate (mg/min) = elimination rate (mg/min)

It's hard to measure the elimination rate, but you can calculate it if you know the clearance and the plasma concentration.

If you give a drug at a steady infusion rate, it will take five half lives to reach steady state at the target plasma concentration (or 96.875% of it at least).

Therefore we usually give a loading dose - which is calculated as follows:

What on earth is context sensitive half life?

Good question.

The graphs we have seen so far generally relate to a single bolus dose of a drug, but things get a little more complex when we start dealing with longer term infusions.

Let's look at propofol

If you infuse propofol for ten minutes and then switch it off, the patient wakes up fairly promptly. If you infuse it for ten hours, the patient takes a lot longer to wake up after you hit stop.

Why?

Propofol accumulates in the fat stores in the body, and then leeches back into the plasma after the infusion stops. This 're-infusion' maintains a certain plasma concentration and prolongs the anaesthetic effect.

The longer the infusion, the longer the effect - the context is simply the duration of the infusion.

Last thing, we promise

Earlier we asked you to bear with us and ignore the whole process of redistribution, and for that we thank you.

Now we can talk about it, and we'll be quick.

The plasma concentration doesn't just drop because of elimination - it also drops because of redistribution, which we've neglected until this point.

This is a graph you need to recognise and understand.

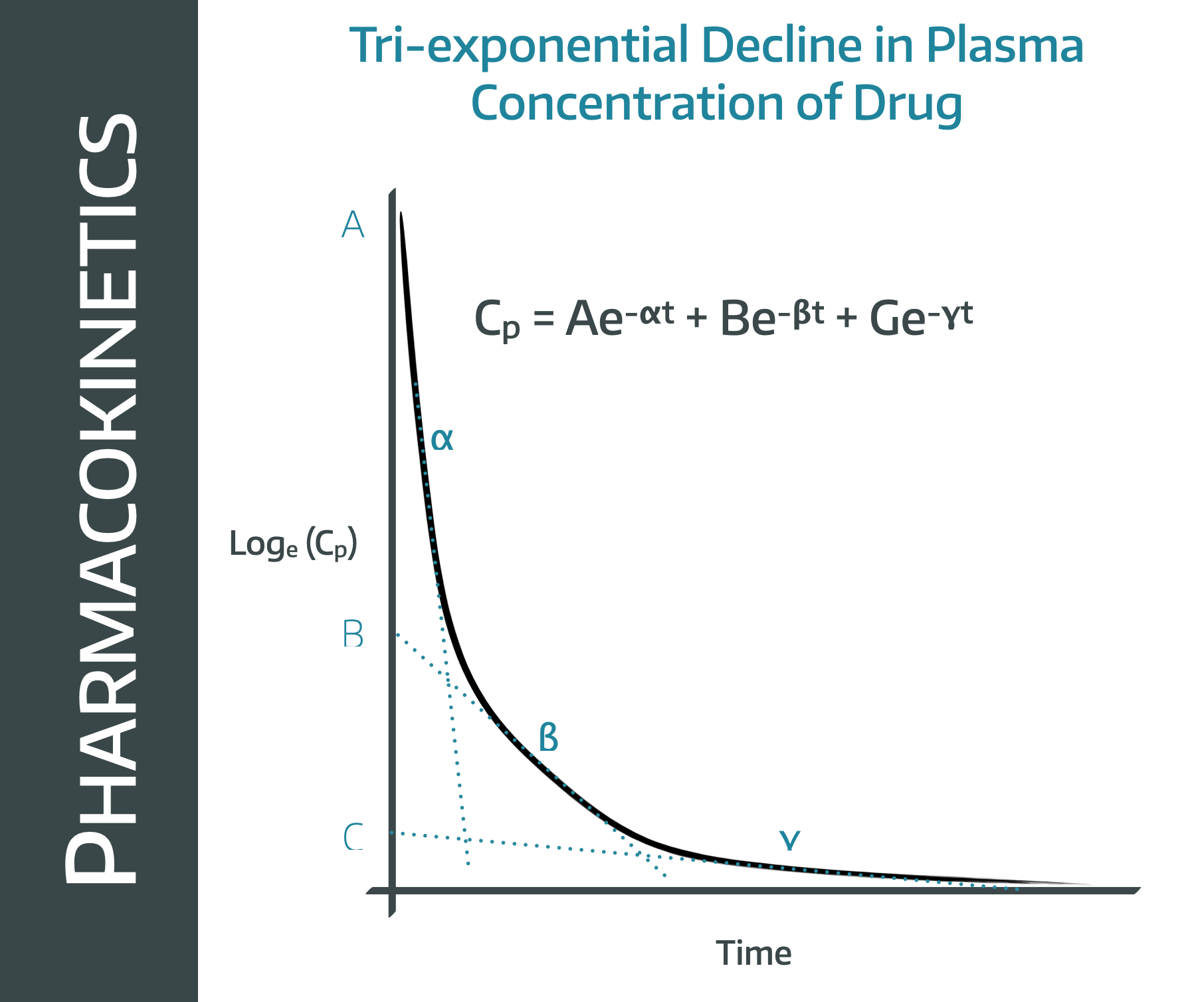
If we look at this graph, it looks a bit like three different curves stuck together, and that's because it is.

Note that this is a log concentration graph, so we'd expect a straight line if it were simple first order kinetics elimination graph.

Instead we have what looks like three straight lines bolted onto one another.

This is because there are three processes going on at the same time, all of which contribute to the fall in plasma concentration over time.

• The drug redistributes into the tissues (the alpha line)
• The drug is eliminated from the plasma (beta)
• The redistributed drug then returns from the tissues into the plasma as we warned it would (gamma)

The first phase gives a very rapid drop in plasma concentration as there is an enormous concentration gradient between plasma and tissues, so lots of molecules redistribute into the tissues fairly quickly.

The second phase represents a steady drop in plasma concentration as the liver and kidneys do their thing. This is the straight line graph from earlier that we've spent pretty much the whole post yapping on about.

In the third phase, the liver and kidneys are still doing their thing, but because the plasma concentration is now lower than the tissue concentration, the molecules start returning to the plasma from the tissue.

This 'autotransfusion' of molecules means the plasma concentration continues to decline, but at a slower rate, hence the gradient isn't quite so steep.

We'll stop talking now.

Useful Tweets and resources

If you want a great video on the reasoning behind the Michaelis-Menten equation, check out this work of art from Andrey K:

Did you know that drug clearance is heavily affected by VV and VA #ECMO: take into account circuit and ECMO factors when evaluating #pharmacokinetics of #antibiotics as explained on this great infographic by 👉 @totalbodydolor 👍 #BEACH2018 #IFAD2018 #FOAMcc #FOAMed pic.twitter.com/TWgPEbHeXI

— Fluid Academy (@Fluid_Academy) November 12, 2018

References and Further Reading

Clearance

Clearance is the efficiency of irreversible elimination of a drug. It is defined as ‘the volume of blood cleared of drug per unit time’; it is the sum of all individual organ clearances (of which the most important are renal clearance and hepatic metabolism). Clearance and elimination are not synonymous. Drug elimination is defined as ‘the amount of drug cleared from the blood per unit time’; in first order kinetics, elimination rate is proportional to dose, while clearance rate remains independent of the dose. In zero-order kinetics, elimination rate is constant.

Deranged PhysiologyAlex Yartsev

Primary FRCA Toolkit

Members receive 60% discount off the FRCA Primary Toolkit. If you have previously purchased a toolkit at full price, please email anaestheasier@gmail.com for a retrospective discount.

Discount is applied as 6 months free membership - please don't hesitate to email Anaestheasier@gmail.com if you have any questions!

Just a quick reminder that all information posted on Anaestheasier.com is for educational purposes only, and it does not constitute medical or clinical advice.